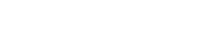Scheduling construction activities
Scheduling construction activties involves chronologically distributing tasks over the available timeframe, determining the resources, durations and procedures necessary to ensure the works are completed in a way that optimises cost, timeframe and quality.
The following basic principles must be understood:
- Labour, both in its various categories and as a whole should be as stable as possible, free of frequent or sudden variations.
- Machinery and additional resources attached to the works should be employed completely.
- The resulting schedule should be clearly understandable, especially to those involved in carrying out the construction works.
The steps taken prior to works scheduling include:
- Detailed study of the design and the site where the construction works are to take place.
- Breakdown of the construction works into activities which depend not just on the type of work to be carried out, but also on the level of intensity. Each activity is measured and evaluated at current market prices.
- Analysis of the existing relationships between the different construction activities, either based on priority or dependency.
- Setting the construction methods and procedures to be followed.
- For every activity the construction procedure is studied, establishing the necessary equipment and calculating their performance levels.
Time is the basic variable in scheduling construction works. The schedule is used to determine the optimal order for the execution of activities. It requires a series of basic steps:
- Identification of interrelationships between tasks.
- Establishing the optimal duration of these tasks.
- Assigning resources to these tasks and establishing load diagrams.
- Obtaining possible dates for each activity and the critical path.
- Verification and adjustment of the scheduling.
The concept of float is used to describe the amount of time that an event or activity can be delayed. The float is obtained by subtracting the duration of a task from the available time.
The critical path is determined by all the events were the total float is zero. As a result, for the activities which comprise the critical path, the earliest and the latest possible dates for the task coincide, both when starting and concluding each activity. The critical activities define the set of tasks which have to be carried out without delay. Any modification in their duration results in an alteration to the critical path and, as a result in the project’s duration.
The duration of an activity can be reduced by adding additional resources, but this will also increase its cost. The “normal” duration of a task is that which minimises its cost. However, a schedule based on normal durations may excessively prolong the work, or may result in the contract duration being exceeded.
In both cases, the duration of some or all of the activities may be reduced by increasing resources, however, there is a minimum possible execution time, even where infinite resources are available. To properly adjust duration, therefore, the time-cost relationship must be known for each activity.
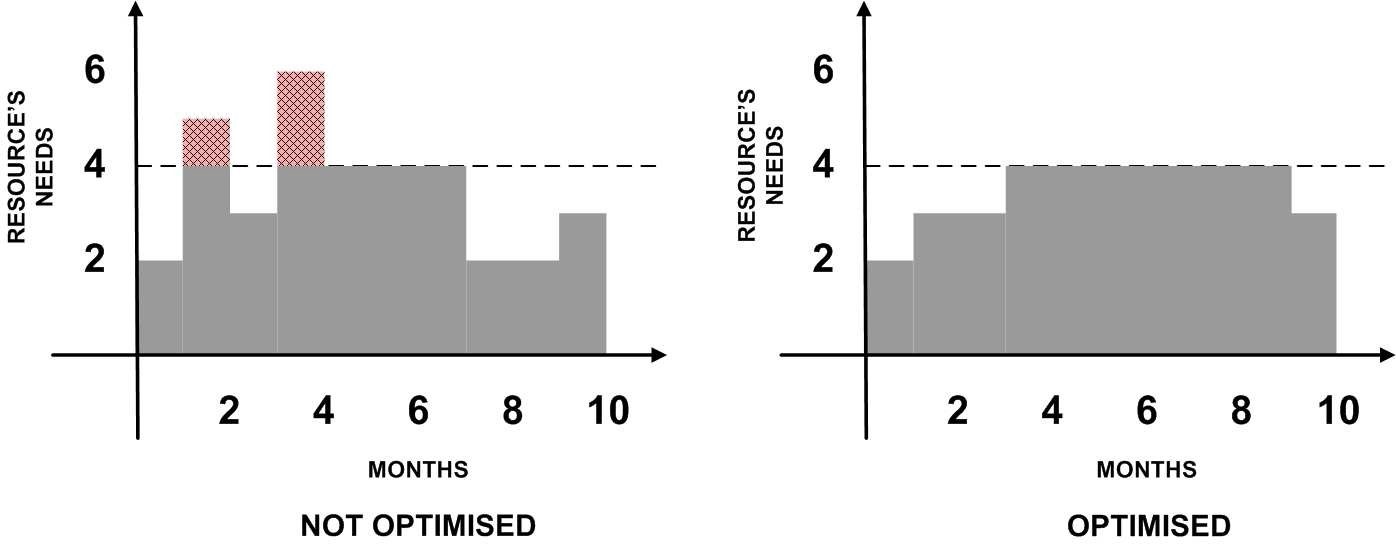
Properly scheduling the available resources is crucial in ensuring that the project is finished within the established timeframe and budget. A load diagram is a useful graphic representation of resources over time, allowing assessment of trends.
Resource limitations result in conflicts which can be addressed using levelling and allocation methods. Levelling evens out the load diagram without delaying the timeframe. Allocation on the other hand ensures that the resources required do not exceed those available, but on the condition that any resulting delay is kept to a minimum. With the help of various network techniques, a critical path is established and floats for each activity determined. The priority in allocating resources will be greater for activities with less available float.
Heuristic methods such as the Burgess-Killebrew method for levelling and the Wiest-Levy method for resource allocation are commonly used and can provide good solutions relatively quickly.
The Burgess-Killebrew algorithm is one of the pioneer algorithms in this field; it is also considered one of the most efficient. The resource load diagram looks for non-critical activities which have the most advanced early completion date. This activity delays its completion by units of time until the float runs out. The earliest completion date for the activity is the one that minimises the sum of squares of resource usage.
This is repeated with all the non-critical tasks, with priority given to those activities with greater float, where the most advanced early completion date for the two tasks coincides. Once completed, a new cycle of repetitions begins until it is impossible to reduce the sum of squares any further.
The Wiest-Levy method is based on the scheduling of activities which can be carried out using the resources available. When the load is greater than the available resource, the activity will have to be delayed; amongst the most non-critical activities, the one that solves the problem with the least delay is chosen. If there are two activities with the same conditions, the one with the greatest float is delayed first, meaning that critical activities are only delayed when there is no other option.
The text in this article is based on an extract from CONSTRUCTION MANAGEMENT, by Eugenio Pellicer, Víctor Yepes, José M.C. Teixeira, Helder Moura and Joaquín Catala. Valencia, Porto, 2008. The original manual is part of the Construction Managers’ Library – created within the Leonardo da Vinci (LdV) project No: PL/06/B/F/PP/174014, entitled: “COMMON LEARNING OUTCOME FOR EUROPEAN MANAGERS IN CONSTRUCTION”. It is reproduced here in a modified form with the kind permission of the Chartered Institute of Building.
--CIOB
[edit] Related articles on Designing Buildings Wiki
- Acceleration of construction works.
- Activity schedule.
- CDM planning period.
- Construction inventory management.
- Construction logistics manager.
- Contractor's master programme.
- Contractor's working schedule.
- Design programme.
- Design web.
- Earned value.
- Fast-track construction.
- Gantt chart.
- How progress is agreed in construction.
- How to manage construction plant.
- Information release schedules.
- Key performance indicators.
- Line of balance (LOB).
- Logic links.
- Logistics management.
- Milestones.
- Phased construction works.
- Precedence diagram method.
- Pre-construction information.
- Programme consultant.
- Progress of construction works.
- Project crashing.
- Resource allocation in design and construction.
- Resource leveling.
- Resource management.
- Short period programme.
- Tender works programme.
- Time-location chart.
- Time management of construction projects.
- Wiest-Levy method.
- Work breakdown structure
[edit] External references
Featured articles and news
Investors in People: CIOB achieves gold
Reflecting a commitment to employees and members.
Scratching beneath the surface; a guide to selection.
ECA 2024 Apprentice of the Year Award
Entries open for submission until May 31.
UK gov apprenticeship funding from April 2024
Brief summary the policy paper updated in March.
For the World Autism Awareness Month of April.
70+ experts appointed to public sector fire safety framework
The Fire Safety (FS2) Framework from LHC Procurement.
Project and programme management codes of practice
CIOB publications for built environment professionals.
The ECA Industry Awards 2024 now open !
Recognising the best in the electrotechnical industry.
Sustainable development concepts decade by decade.
The regenerative structural engineer
A call for design that will repair the natural world.
Buildings that mimic the restorative aspects found in nature.
CIAT publishes Principal Designer Competency Framework
For those considering applying for registration as a PD.
BSRIA Building Reg's guidance: The second staircase
An overview focusing on aspects which most affect the building services industry.
Design codes and pattern books
Harmonious proportions and golden sections.
Introducing or next Guest Editor Arun Baybars
Practising architect and design panel review member.
Quick summary by size, shape, test, material, use or bonding..