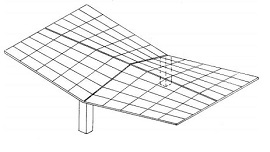
Hyperbolic paraboloid in construction
|
|
|
|
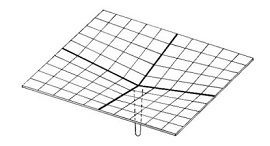
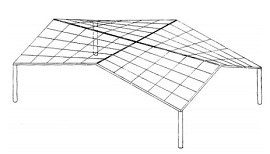
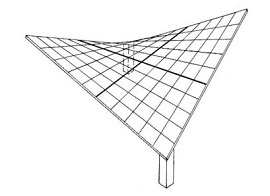
A hyperbolic paraboloid (sometimes referred to as ‘h/p’) is a doubly-curved surface that resembles the shape of a saddle, that is, it has a convex form along one axis, and a concave form on along the other. It is also a doubly-ruled surface, that is, every point on its surface lies on two straight lines across the surface. Horizontal sections taken through the surface are hyperbolic in format and vertical sections are parabolic.
The fact that hyperbolic paraboloids are doubly-ruled means that they are easy to construct using a series of straight structural members. As a consequence they are commonly used to construct thin ‘shell’ roofs. These can either be formed using timber or steel sections, that are then clad, or they can be constructed using concrete.
The use of hyperbolic paraboloids as a form of thin shell construction was pioneered in the post-war era, as a hybrid of modern architecture and structural engineering. Being both lightweight and efficient, the form was used as a means of minimising materials and increasing structural performance while also creating impressive and seemingly complex designs.
Rather than deriving their strength from mass, like many conventional roofs, thin shell roofs gain strength through their shape. The curvature of the shape reduces its tendency to buckle in compression (as a flat plane would) and means that they can achieve exceptional stiffness. Being braced in two directions they experience no bending and are able to withstand unequal loading, whether from dead loads (such as equipment hung from the ceiling), or live loads (such as wind).
Hyperbolic paraboloid shell roofs can be constructed using reinforced concrete with a shell thickness of just 50 mm for diagonal spans up to 35 m.
[edit] Related articles on Designing Buildings Wiki
- Anticlastic.
- Arches.
- Barrel vault.
- Cantilever.
- Catenary.
- Concept structural design of buildings.
- Conoid shell.
- Folded plate construction.
- Long span roof.
- Megastructure.
- Pendentive dome.
- Portal frame.
- Shell roof.
- Structural engineer.
- Synclastic.
- Tensegrity.
- Tensegrity bamboo pavilion
- Tensile structures.
- The development of structural membranes.
- Types of dome.
[edit] External resources
- ‘Building Construction Handbook’ (6th ed.), CHUDLEY, R., GREENO, R., Butterworth-Heinemann (2007)
Featured articles and news
One of the most impressive Victorian architects. Book review.
RTPI leader to become new CIOB Chief Executive Officer
Dr Victoria Hills MRTPI, FICE to take over after Caroline Gumble’s departure.
Social and affordable housing, a long term plan for delivery
The “Delivering a Decade of Renewal for Social and Affordable Housing” strategy sets out future path.
A change to adoptive architecture
Effects of global weather warming on architectural detailing, material choice and human interaction.
The proposed publicly owned and backed subsidiary of Homes England, to facilitate new homes.
How big is the problem and what can we do to mitigate the effects?
Overheating guidance and tools for building designers
A number of cool guides to help with the heat.
The UK's Modern Industrial Strategy: A 10 year plan
Previous consultation criticism, current key elements and general support with some persisting reservations.
Building Safety Regulator reforms
New roles, new staff and a new fast track service pave the way for a single construction regulator.
Architectural Technologist CPDs and Communications
CIAT CPD… and how you can do it!
Cooling centres and cool spaces
Managing extreme heat in cities by directing the public to places for heat stress relief and water sources.
Winter gardens: A brief history and warm variations
Extending the season with glass in different forms and terms.
Restoring Great Yarmouth's Winter Gardens
Transforming one of the least sustainable constructions imaginable.
Construction Skills Mission Board launch sector drive
Newly formed government and industry collaboration set strategy for recruiting an additional 100,000 construction workers a year.
New Architects Code comes into effect in September 2025
ARB Architects Code of Conduct and Practice available with ongoing consultation regarding guidance.
Welsh Skills Body (Medr) launches ambitious plan
The new skills body brings together funding and regulation of tertiary education and research for the devolved nation.
Paul Gandy FCIOB announced as next CIOB President
Former Tilbury Douglas CEO takes helm.