Running mean temperature
When people are dissatisfied with their thermal environment, not only is it a potential health hazard, it also impacts on their ability to function effectively, their satisfaction at work, the likelihood they will remain a customer and so on.
Thermal comfort is dependent on environmental factors, such as air temperature, air velocity, relative humidity and the uniformity of conditions, as well as personal factors such as clothing, metabolic heat, acclimatisation, state of health, expectations, and even access to food and drink.
In the 1970s the existing, ‘steady-state’ theory of comfort was challenged by an adaptive comfort theory which suggested that comfort was time dependent, as the occupants of a building would adapt to their environment over time, adjusting clothing, modifying behaviour and so on. This suggested that the occupants of a building might actually accept conditions that would otherwise have been predicted to be unsatisfactory.
It was proposed that an exponentially-weighted outside running mean temperature could account for this time-dependency.
The equation for the exponentially-weighted running mean temperature for time T is:
Trm = (1-α){T(t-1) + αT(t-2) + α²T(t-3)…..}
Were Tn is the temperature at each time interval, and α is a constant between 0 and 1. The temperatures Tn become less significant as time progresses, with the speed of decay depending on the value of the constant α. The lower the value of α, the less significant the weighting of past temperatures.
[edit] Related articles on Designing Buildings Wiki
Featured articles and news
Latest Build UK Building Safety Regime explainer published
Key elements in one short, now updated document.
UKGBC launch the UK Climate Resilience Roadmap
First guidance of its kind on direct climate impacts for the built environment and how it can adapt.
CLC Health, Safety and Wellbeing Strategy 2025
Launched by the Minister for Industry to look at fatalities on site, improving mental health and other issues.
One of the most impressive Victorian architects. Book review.
Common Assessment Standard now with building safety
New CAS update now includes mandatory building safety questions.
RTPI leader to become new CIOB Chief Executive Officer
Dr Victoria Hills MRTPI, FICE to take over after Caroline Gumble’s departure.
Social and affordable housing, a long term plan for delivery
The “Delivering a Decade of Renewal for Social and Affordable Housing” strategy sets out future path.
A change to adoptive architecture
Effects of global weather warming on architectural detailing, material choice and human interaction.
The proposed publicly owned and backed subsidiary of Homes England, to facilitate new homes.
How big is the problem and what can we do to mitigate the effects?
Overheating guidance and tools for building designers
A number of cool guides to help with the heat.
The UK's Modern Industrial Strategy: A 10 year plan
Previous consultation criticism, current key elements and general support with some persisting reservations.
Building Safety Regulator reforms
New roles, new staff and a new fast track service pave the way for a single construction regulator.
Architectural Technologist CPDs and Communications
CIAT CPD… and how you can do it!
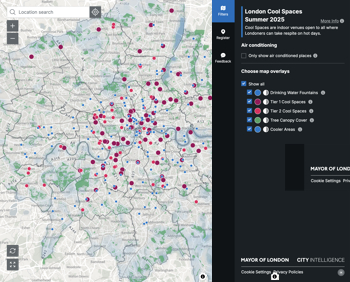
Cooling centres and cool spaces
Managing extreme heat in cities by directing the public to places for heat stress relief and water sources.
Winter gardens: A brief history and warm variations
Extending the season with glass in different forms and terms.
Restoring Great Yarmouth's Winter Gardens
Transforming one of the least sustainable constructions imaginable.