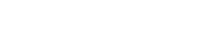Drawing projections
There are a number of techniques of projection that can be used to represent three-dimensional objects in two-dimensions by 'projecting' their image onto a planar surface.
Drawing projections should comply with relevant standards (such as British Standards) to prevent misunderstanding and avoid errors in interpreting the drawing.
Contents |
[edit] Orthographic projection
Orthographic projection is a type of 'parallel' projection in which the four orthogonal views of an object are shown. The orthographic projection commonly used in the UK is called first angle projection.
[edit] Axonometric projection
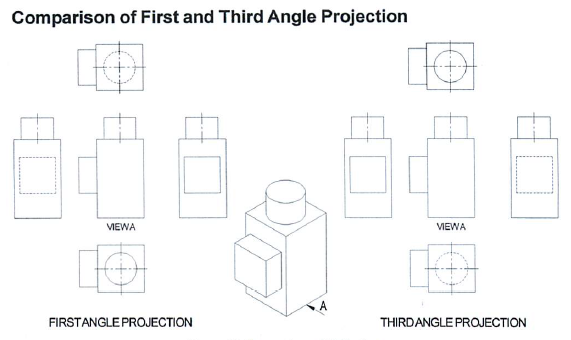
Axonometric projection creates a true plan set at 45º, which retains the original orthogonal geometry of the plan. It is particularly suitable for representing interior designs, such as kitchen layouts. Planning drawings can also be effective represented as axonometric projections, showing the relationships between buildings and topography.
The axonometric method became increasingly popular in the 20th century as a formal presentation technique, but recently has become less widely used due to the emergence of CAD programmes and building information modelling.
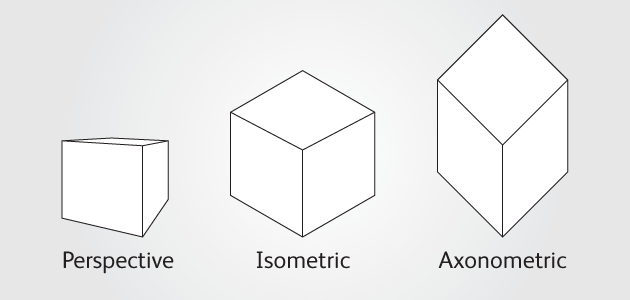
NB Drawing for Understanding, Creating Interpretive Drawings of Historic Buildings, published by Historic England in 2016 suggests that axonometric projection: 'Is a type of parallel projection used for creating a drawing where the plan is drawn to scale but rotated at an angle of 60° or 30°along one or more of its axes relative to the normal axis.'
[edit] Isometric projection
The isometric was the standard view until the mid-20th century. Unlike the axonometric projection, the isometric plan view is slightly distorted, using a plan grid at 30º from the horizontal in both directions. It can be used to show the nature of the design and explain construction details more clearly than an orthographic projection. It is sometimes used during concept design to help the client grasp the mass of the proposal.
[edit] Oblique projection
When primary information is drawn in elevation, the interpretation can be enhanced by an oblique projection. This is a simple method of producing two-dimensional images of three-dimensional objects. The differentiating characteristic of oblique projection is that the drawn objects are not in perspective, and so do not correspond to any actual obtainable view.
[edit] Parallel projection
'Parallel projections have lines of projection that are parallel both in reality and in the projection plane.' Ref Drawing for Understanding, Creating Interpretive Drawings of Historic Buildings, published by Historic England in 2016.
[edit] Related articles on Designing Buildings Wiki
- Architectural reprography.
- As-built drawings and record drawings.
- Assembly drawing.
- Augmented reality in construction.
- Bill of quantities.
- Blueprint.
- Building information modelling.
- CAD layer.
- Component drawing.
- Computer aided design.
- Concept drawing.
- ConTech.
- Detail drawing.
- Elevations.
- Engineering drawing.
- Exploded view.
- General arrangement drawing.
- Geometric form.
- How to draw a floor plan.
- Installation drawings.
- Manual drafting techniques.
- North American Paper Sizes
- Notation and symbols.
- Orthogonal plan.
- Paper sizes (ISO 216 A, B and C series)
- Production information.
- Section drawing.
- Shop drawings.
- Site plan.
- Specification.
- Technical drawing.
- Types of drawings.
- Working drawing.
Featured articles and news
ECA 2024 Apprentice of the Year Award
Entries open for submission until May 31.
UK gov apprenticeship funding from April 2024
Brief summary the policy paper updated in March.
For the World Autism Awareness Month of April.
70+ experts appointed to public sector fire safety framework
The Fire Safety (FS2) Framework from LHC Procurement.
Project and programme management codes of practice
CIOB publications for built environment professionals.
The ECA Industry Awards 2024 now open !
Recognising the best in the electrotechnical industry.
Sustainable development concepts decade by decade.
The regenerative structural engineer
A call for design that will repair the natural world.
Buildings that mimic the restorative aspects found in nature.
CIAT publishes Principal Designer Competency Framework
For those considering applying for registration as a PD.
BSRIA Building Reg's guidance: The second staircase
An overview focusing on aspects which most affect the building services industry.
Design codes and pattern books
Harmonious proportions and golden sections.
Introducing or next Guest Editor Arun Baybars
Practising architect and design panel review member.
Quick summary by size, shape, test, material, use or bonding..